Products
DEPOSITION TOOLSPlasma Enhanced Chemical Vapour Deposition (PECVD)Inductively Coupled Plasma Chemical Vapour Deposition (ICPCVD)Atomic Layer Deposition (ALD)Ion Beam Deposition (IBD)ETCH TOOLSInductively Coupled Plasma Etching (ICP RIE)Reactive Ion Etching (RIE)Deep Silicon Etching (DSiE)Atomic Layer Etching (ALE)Ion Beam Etching (IBE)
Learning


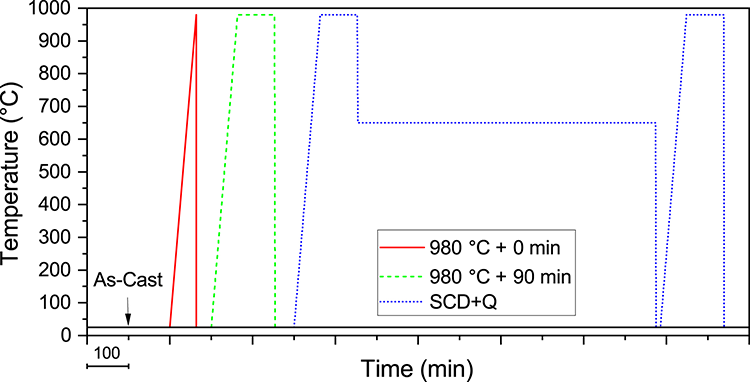 Figure 1. Schematic of the four different heat treatments performed on the HCCI samples.
Figure 1. Schematic of the four different heat treatments performed on the HCCI samples.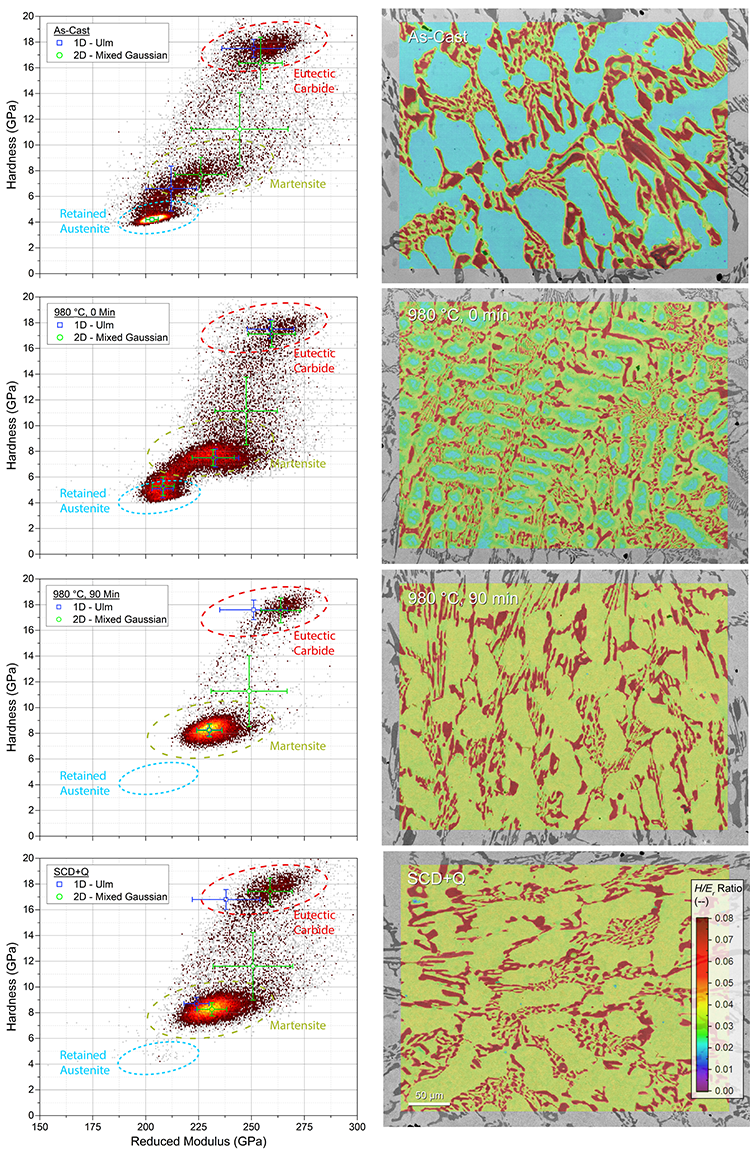 Figure 2. 2D histograms and H/Er ratio maps showing the evolution of the microstructures and their properties as a function of heat treatment with the phase regions labeled and statistical/cluster locations and standard deviations.
Figure 2. 2D histograms and H/Er ratio maps showing the evolution of the microstructures and their properties as a function of heat treatment with the phase regions labeled and statistical/cluster locations and standard deviations.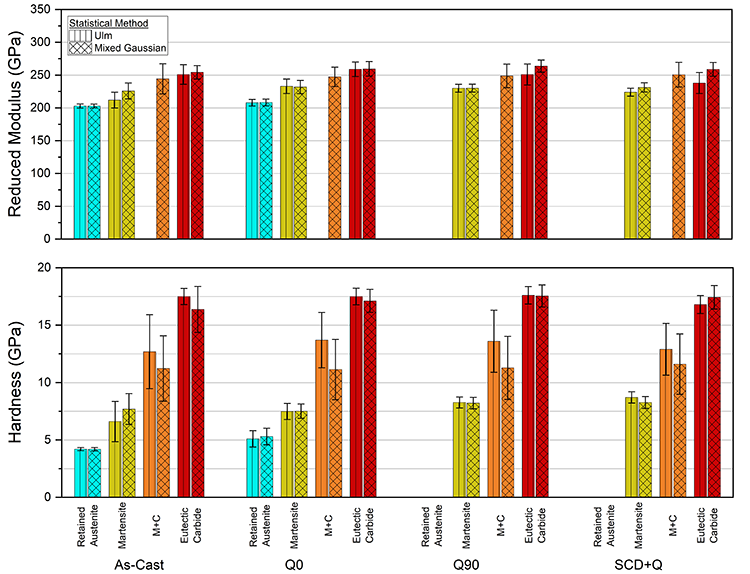 Figure 3. Phase-level properties as a function of heat treatment and segmentation method.
Figure 3. Phase-level properties as a function of heat treatment and segmentation method.